Using Z and T-Tests for eCommerce A/B Evaluation
Using Z and T Tests for eCommerce A/B Evaluations

Introduction
I recently interviewed for a data science position at a company with a large eCommerce presence. In the interview, the topic of A/B testing came up. The company has a large online presence, and is looking for was to maximize their search and recommendation features online. A common approach for evaluating different changes to search algorithms (or really any other kind of UX change that affect site visitors) is to use A/B testing. In A/B tests, web traffic gets split between a control group, and a group that experience the proposed changes. Results are then gathered from the two “treatments”, and compared. This presents an excellent opportunity to use some of the tools of statistics to state, with a certain level of confidence, if the changes are having the desired effect.
In this blog post, I will look at two different types of tests that can be used with web based A/B testing, and in particular testing related to eCommerce search scenarios. Those tests will be a Z test, and a T-Test. So, let’s get to it…
Z Testing
Jesse Farmer has posted an excellent blog entry on the topic of statistical analysis of A/B testing. I highly recommend it. This post will follow a similar approach that Farmer uses in his article. However, one slight difference is that the scenario that I am looking at is focused on web users clicking on a search result in a list, rather than membership conversion.
Some background information:
NOTE: THE FOLLOWING EXAMPLE IS NOT REAL. THE DATA HAS BEEN GENERATED IN ORDER TO EXPLORE THE TOPIC. ANY SIMILARITIES TO EXISTING SEARCH RESULTS AT ANY COMPANY IS COMPLETELY COINCIDENTAL!
A company with a large web presence for selling items has recently made a change to their searching algorithm. The company then collected data from the website with a partial split between the normal approach that they have been using for displaying search results, and a new approach. We will call these approaches “A” and “B” respectively. What we want to be able to show is that with a 95% level of confidence that the new search algorithm results in more users clicking on a search result to view the details of a product (and eventually buy it) than the old approach.
| Treatment | Impressions | Click-through | Percent Score |
| "A" | 10,000 | 219 | 2.19% |
| "B" | 10,000 | 289 | 2.89% |
For our test, we will establish a null hypothesis that the click-through rate of our control is no less than the click-through rate of our new algorithm. (i.e. p ≤ pc ).
We formally write the null hypothesis as:
Ho : p - pc ≤ 0
Here pc is the click-through rate of the control group and p is the click-thru rate that we observe when running our new algorithm.
The next step is to create a new distribution, X. We create this distribution based on the p and pc that we used in the previous step.
X = p - pc
Our null hypothesis is now:
Ho : X ≤ 0
We did this because we know that X is normally distributed. We know that because both p and pc were normally distributed and the difference between two normally distributed random variables is also normally distributed. (It has to be true because its on wikipedia.… Penn state also agrees.
To see if we fall inside the 95% confidence interval, we need to compute the following:
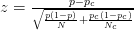
where N is the sample size of the experimental treatment and Nc is the sample size of the control set.

We then compare that value (3.18) to the value of P on the normal distribution for a one tailed test at 95% confidence, which is 1.645. The value falls in the critical region, which means that it is “statistically significant.”
A statistically significant result means the we can reject the null hypothesis and state with 95% confidence that our new search algorithm does result in more click-throughs than the old algorithm.
It is kind of a no-brainer, if you look at the data. The results went up from 2.19% to 2.89% and our sample size was rather large.
Z-Test Example 2
Let’s now look at a similar example, but with a much smaller sample size…
Number of impressions: 100 Length of A: 19 Length of B: 32
Rather than re-calculating this by hand, not that that was not fun, I am going to use this site that has a handy proportion tester. When I do that, I can see that the p-value and Z-Score for my data are:
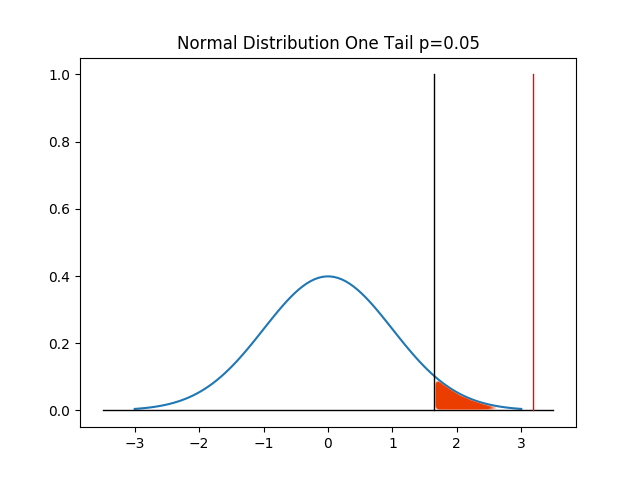
The Z-Score is 2.109. The p-value is 0.01743.
Next we need the value of Z for a 95% confidence interval. Looking in my trusty copy of “Introduction to Probability and Statistics, Second Edition” by Milton and Arnold (ISBN: 0-07-042353-9), I can see that the Z value is 1.64 (approximately.) Because 1.64 < 2.109, my results are statistically significant.
Here is a graph that shows how the calculated Z falls outside of the 95% interval.
Therefore, I can reject H0 at the 95% level. In other words, I can say with 95% confidence that the changes in my A/B test are working.
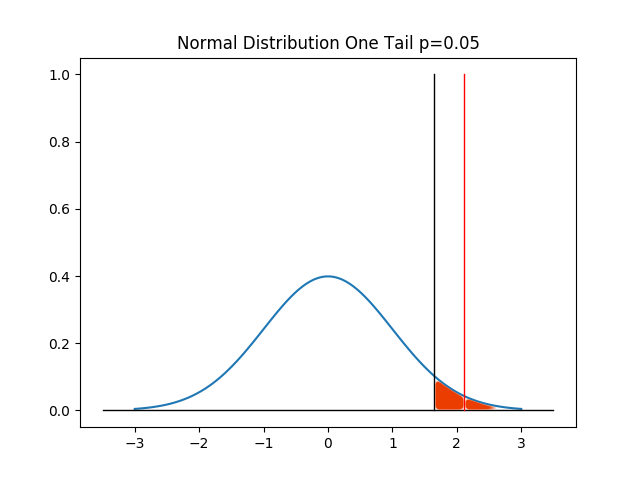
However, if we increase the confidence interval of the test to 99%, the needed Z score now shifts to 2.33. And, because 2.33 > 2.109, I cannot reject H0 at the 99% level.
That’s great, but we can even go a bit further… what if we consider the average amount of the sale in each sample as well…
T-Testing
When people search for products on a website, it is great to know if they are more likely to click through to product details based on search results. That said, it is even better to know if they tend to buy higher priced products. One way that we can do this kind of testing is to use a T-Test. T-tests provide a way for us to take two samples and, based on their means, be able to make statements regarding if the two samples are coming from the same population. In terms of A/B testing, we frame the question slightly differently and use T tests to make statements about how observed behavior has changed.
If we consider the same above tests we would also start to look at the average purchase amounts that have resulted from two different search algorithms.
Consider this table of data…
Number of impressions: 100
Length of A: 27
Average A sale: 347.45713926561115
Length of B: 24
Average B sale: 355.1043836727288
Here is a nice histogram that summarizes the results of our test..
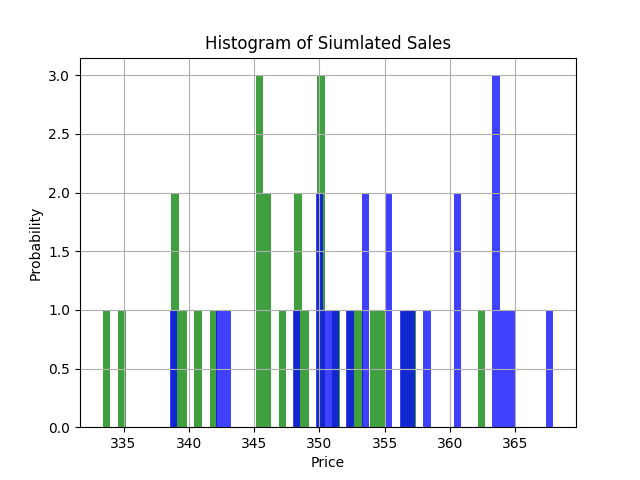
Now, let’s set up a t test to compare the sample means between the two groups. First, we need a null hypothesis:
For the T-Test, we start with a null hypothesis that the two sample means (average sale in the above) are the same.
H0 : µ1 = µ2
The alternative hypothesis is that they are not the same:
Ha : µ1 ≠ µ2
We can compute the test statistic with the following formula:
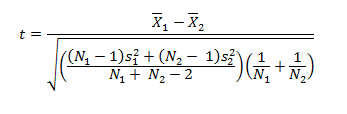
Now, I could do this calculation by hand… or I can use this handy online calculator to compute the result for me:
The t-value is -3.72547. The p-value is .000252. The result is significant at p < .05.
Because the result is statistically significant (or our t-value falls in the critical region) we reject the null hypothesis that the two samples come from populations with the same mean.
What is this telling us? It says that our changes between A and B have affected the average amount that people spend on items based on our data.
Note: Code for this site is available in the following git repo:
https://github.com/fractalbass/ab_t_test.git
Conclusion
Both Z and T tests provide useful tools for evaluating the performance of A/B tests. Using these tools helps us determine the statistical significance (confidence intervals) for the results of the tests and help account for the fact that the underlying data in these tests is sampled, and is also randomly distributed.
I hope you have enjoyed this blog post on using Z and T tests for evaluating the results of e-commerce A/B testing. Please check back soon for more posts on topics related to data science.
References:
Social Science Statistics Calculator
Random Variables Discussion on Wikipedia
Penn state online course on stats
Blog entry by Jesse Farmer on Statistical Analysis of A/B Testing